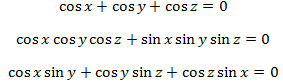大家一起做多孔螺旋型與鑽石型三度週期最小曲面的串珠模型(上)—立體幾何介紹/左家靜、莊宸、金必耀
大家一起做多孔螺旋型與鑽石型三度週期
最小曲面的串珠模型(上)—立體幾何介紹
左家靜a、莊宸b、金必耀*c
a國家高速網路與計算中心、b美國麻省理工學院化學系、*c國立臺灣大學化學系
*[email protected]
n摘要
動手做可以有效增進數學與化學的學習成效,本文介紹一種模組化方式,讓大家能一起動手製做兩種結構優美的三度週期最小曲面的串珠模型:多孔螺旋型與鑽石型類石墨烯體。我們將這兩類曲面分解成相同的螺旋長條型帶子,可以分別進行製作,最後再以兩種不同的方式連結,製作成含有約八個晶胞的兩種2 x 2 x 2多孔類石墨烯體,所製成的串珠模型不但形態優美結構精巧,更是一個具有數學與科學內涵的藝術品。
關鍵字:物理模型、分子模型、串珠模型、三度週期最小曲面、多孔螺旋最小曲面、鑽石型最小曲面、石墨烯結構
n引言
你知道蝴蝶的翅膀為什麼看起來那麼地絢麗嗎?你知道為什麼手指頭長時間泡在水中只會產生皺紋,而不會融化在水中嗎?這些有趣而且重要的現象,其實都跟奈米尺度的多孔螺旋週期結構(gyroidal structures)有關1-5。
瞭解物質在奈米尺度的結構、性質、與其變化是化學研究的核心問題,但是弄清楚奈米尺度的各種結構特徵是不是一件容易的事情。例如,雖然平面的石墨烯結構容易理解,僅是一個六邊形的蜂窩排列,但是由石墨烯所延伸出來的多孔週期立體結構,像是多孔碳舒瓦玆體(carbon Schwarzites)或是碳海綿體(carbon sponge)微觀細部與整體構造並不是那麼容易想像。一個辦法是模型的建構,通過製作巨觀的模型,可以增進我們對奈米尺度立體結構的認識6,7。
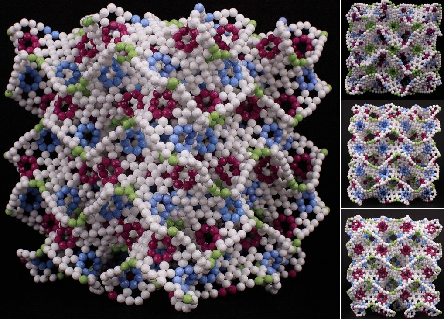
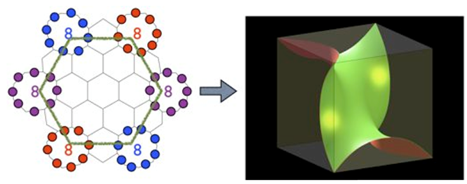
本文介紹兩種多孔碳舒瓦玆體的串珠模型製作,這種結構也可稱為多孔碳石墨烯體,這兩種結構分別為多孔螺旋結構(簡稱G型,參見圖1)與鑽石型結構(簡稱D型),均屬於三度週期最小曲面(Triply Periodic Minimal Surfaces,TPMS),也是雙曲面型的曲面,雖然僅有少數實驗室能夠合成類似本文所討論的多孔碳石墨烯體,但是週期最小曲面等幾何結構是普遍存在於自然界以及一些高分子體系中,所以通過多孔石墨烯體的模型建構,我們可以對於此類雙曲面型的非歐幾何奈米結構有一些初步的認識3,6,7。
圖1:多孔螺旋結構型三度週期最小曲面
在國際化學年的最後兩個月,本文作者曾與北一女數位化學科的老師以及三個班的同學一起合作,利用模組化方式,成功地製作出一大一小兩個含有6750的超級珠璣碳球C4500。這證明,雖然串珠是一個循序的建構過程,但是通過適當的分解,也可以將複雜的串珠過程,分解成簡單的單元,可由大家合力動手做,在很短的時間內,做出極富數學與科學意涵的串珠雕塑。除了超級珠璣球可以分解為較為簡單易做的單元,三度週期最小曲面的串珠結構經過適當的分解,也可以產生結構單純,易於製做的單體螺旋長帶,如此,縱然僅有初步經驗的一些串珠初學者,也可以按圖索驥,一起合作,製做出驚人的串珠幾何藝術品8-17。
除了D型與G型最小曲面,還有一個結構更為單純的三度週期最小曲面,叫做P型曲面,但由於P型曲面串珠模型的分解方式,跟D型與G型曲面不一樣,所以本文將以G型與D型最小曲面串珠模型的製做為主。製作程序分為兩個部份:第一是單體的製做,這個部分可以由許多人一起製作;第二是單體的連結與組裝,以兩種不同的連結方式,可分別產生D型與G型兩種三度週期最小曲面。在這三種最小曲面中,G曲面特別的不易想像,這是因為此結構中沒有鏡面對稱,在曲面上找不到直線;而P與D曲面則有鏡像對稱,以及可清楚判斷的結構單元,因此本文作者很早就成功地利用一個單元一個單元的構築方式,建構起此兩結構的串珠模型,唯獨G型曲面特別困難,一直到本文作者發展出以螺旋長帶為單元的模組方法後,才終於成功製作出此結構的串珠模型。
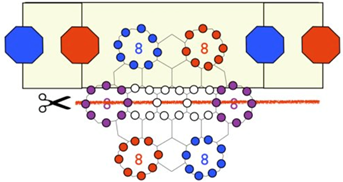
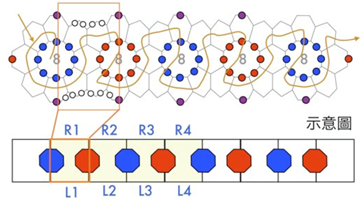
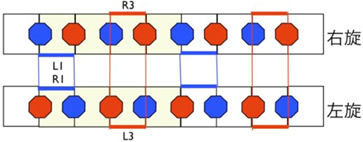
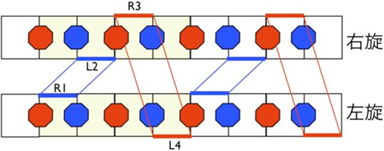
第二階段為單體的連結,這是整個製作過程中最困難的地方,每一個單體為一條螺旋長帶,相鄰的兩個長帶不僅只在同一側相連,而是一條長帶兩側都與相鄰另一個長帶的兩側都有連結,讀者也許會懷疑,如果一長帶的左側已經與鄰帶相連結,右側怎麼可能再與同一鄰帶相連結。如果長帶攤平在一平面上,那確實是不可能的,但是空間是立體的,若允許長帶在三度空間旋轉成一螺旋帶,則可能同時在長帶的兩側都與鄰帶的兩側相連接。
因此對於D型與G型兩種最小曲面的結構特徵,有一些基本認識,才能避免產生錯誤。串珠模型製作的一個困擾是,一旦發生錯誤,特別是發生在比較久以前的錯誤,是很不容易進行修改的。我們在下兩節對三度週期最小曲面最些基本的介紹,然後才進入到串珠結構的單體,以及雙體連結規律。
n背景知識
21+κ2,所對應的高斯曲率一定是負的,非平的最小曲面必然處處都是鞍點。
舒瓦玆不等式。P型曲面是第一個三度延伸、沒有邊界的週期最小曲面,由於的結構單元與正立方體有相同的對稱,比起其他三度最小曲面還要簡單而基本,所以舒瓦玆稱此曲面為原型(Primitive),表示其重要性。D型曲面的結構則與鑽石的結構類似,所以稱為鑽石型(Diamond)的最小曲面。P與D型曲面在自然界中的許多微觀結構中都很常出現,化學家也能夠通過化學合成設計出各種有用的多孔洞沸石結構,由於含有大量的孔洞,所以沸石常具有非常好的催化用途,常被應用到各種化學相關的產業中。
圖2:三種基本的三度週期最小曲面,由左至右本別是P型、G型、D型三度週期最小曲面。
富勒的尊崇,由於發現此類分子對奈米科技的重要性,1996年的諾貝爾化學獎頒給了R. Smally、R. Curl、H. Kroto三位化學家。
引入五邊形可以產生正的高斯曲率,但引入是大於六的七邊形或是八邊形,則會產生相反的影響,在石墨烯平面上引入負的高斯曲率,對應到的是鞍點。處處為負的曲面不像正曲面,不會形成籠形的封閉球體,而是無限延伸的曲面,數學家將這種負曲面叫做雙曲面型的曲面。在石墨烯適當的週期位置上引入八邊形,可以產生近似各種三度週期最小曲面的石墨烯結構,我們稱這些三度空間無限延伸的單層石墨烯為「類石墨烯體」(graphenoid)或是「碳舒瓦玆結構」,用以表達對數學家十九世紀德國數學家舒瓦玆(H. Schwarz)的尊敬。
我們在下一節會針對P、D、G三種曲面的幾何做簡單的介紹,然後在下一篇文章說明如何用適當模組化方式,把整個編織過程分解成許多簡單的單元,進行組裝。
nP、D、G三度週期最小曲面的結構
的意義是以螺旋的方式行進,因此佘恩稱這種三度週期最小曲面為gyroid,直譯為「類螺進體」。另外還有一個一維的最小曲面稱為helicoid,可譯為「類螺旋體」。本文將gyroid譯為「多孔螺旋三度週期最小曲面」,或簡稱為「多孔螺旋曲面」、「多孔類螺旋體」。
一般來說,要利用魏爾斯特拉斯方程來產生這三種曲面的空間圖像,需要用到複數積分,並非易事。 然而我們可以用下列三個三角函數的隱函數方程式,分別來近似P、D、G三種曲面:
利用這些三角函數的隱函數公式,我們在圖二繪出這三個曲面的近似結構,讀者應該不難看出這些曲面的基本特徵。現在的計算機上有許多現成的數學繪圖軟體,可以直接輸入公式,就產生隱函數方程式所對應的三度空間曲面。本文的3D模擬圖皆是利用matlab軟體所繪製的,其他像是蘋果電腦上所附的grapher也可以輕鬆繪出這些曲面,若是能夠配合動態的旋轉,可以更容易認識這些曲面的立體結構。
的改變,曲面並沒有發生擠壓或是伸張,用數學術語來說,這種變換是等度量的(isometric)。這一點會反應在最後我們所做出來的近似串珠三度週期最小曲面上,也就是這三種曲面的類石墨烯體的局部結構基本上是一樣的。
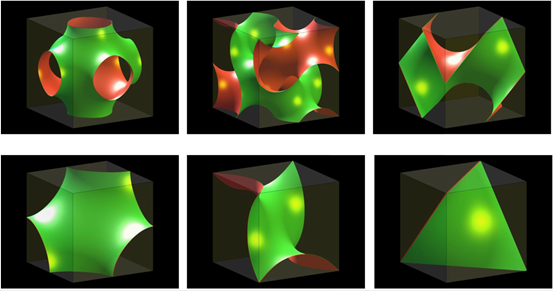
我們在圖2中依序繪出含有2 x 2 x 2八個單元的P與G曲面,以及含有1 x 1 x 1一個單元的D曲面。而在圖2中的第一列,我們給出含有1 x 1 x 1一個晶胞的P與G曲面,以及含有1/8個晶胞的D曲面;圖3的第二列則是再將第一列的大小縮小為其1/8。
圖3:P、G、D型三度週期最小曲面。第一列含有個晶胞;第二列則是一個晶胞;第三列則是不可進一步化約的最小的重複單元。
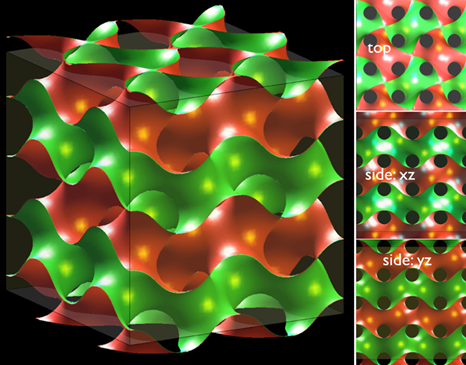
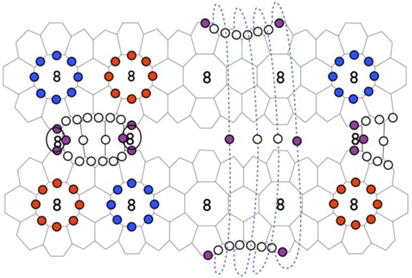
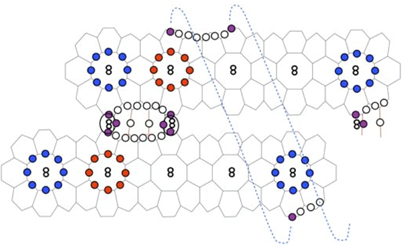
實際在製作最小曲面時,我們不可能製作一個真正無限延伸的體系,那會佔滿整個世界,我們的目標是製作一個2 x 2 x 2八個單元的模型,這可以有許多的可能選擇,圖2與圖3所示僅是一種可能的情形,由於基本長條單元的選擇,我們將製作的多孔螺旋型以及鑽石曲面的串珠模型,與圖2及圖3中的G型與D型曲面切割方式會有些出入,以G型曲面串珠模型為例,實際上比較接近圖3中所切割的G型曲面,上面與兩個側面xz與yz所切的位置稍有不同,所以整個結構並非是正立方體,而時稍微向z方向延長一些。圖4的右側,我麼也給出與xz、yz平行的側切面,以及與xy平面平行的上切面,四個側切面與上下兩切面的紋路並不一樣。
圖4:多孔螺旋最小曲面:這是本計劃所將製作實際的串珠模型,比2 x 2 x 2八個晶胞沿z方向上下各多出約0.25個單位,實際所對應到的G曲面區域,以及從三個方向朝此區域所看到的圖像,讀者可以跟首頁的串珠模型圖相比較。
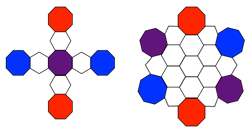
我們還刻意地繪晶胞所對應的立方體,方便讀者的想像,這三個週期最小曲面在晶胞邊緣上的曲線形狀。特別是在圖二中,最小的單元對應到一個所謂的猴子鞍點(monkey saddle)。在這些點附近,曲面是平的,兩個主曲率皆為零,有時稱為平點(flat points)。對應到的「類石墨烯體」模型,在平點附近會用由一個蔻(coronene)的結構來近似(圖5),蔻的中文有幾種不同的翻譯,例如暈苯、六苯並苯、蔻。環繞在蔻周圍有六個八邊形,分別交替地朝向x、y、z方向,這個結構特徵可以當做製作串珠模型時,隨時用以檢查結構是否正確。由於所有的八邊型是完全是全等的,不同的是有三分之一的八邊型面向x方向,另外三分之一則朝向y方向,剩下的則朝向z方向,所以可以用顏色來區分這三類的八邊形,如圖5所示,我們分別用藍、紅、紫三種顏色來區別,以方便製作時,隨時檢查之用。讀者完全可以有自己所設計的配色方式,這也是串珠模型與一般分子模型一個不一樣的地方,相同的分子模型,可以有各種配色方法,以呈現製作者對色彩的感覺與想法。
圖5:猴子鞍點由一個六苯並苯結構單元近似。猴子鞍點(monkey saddle)與一般常見的鞍點(saddle)步一樣,一般的鞍點是在馬的背部,人坐上去,兩腳橫跨在兩側,前後的方向向上。但是這種鞍點不適合猴子來乘坐,因為猴子有一條長長的尾巴,所以除了兩個向下方向讓腳橫跨,還需要第三個方向讓尾巴垂下,圖右所示便是多孔螺旋週期最小曲面中的這種猴子鞍點。
n結論
本文介紹P、D、G三種週期最小曲面的立體幾何,以及曲面的平均與高斯曲率等相關概念。對這些立體幾何的初步認識有助於建構這些模型的實作,對於了解這類型奈米材料的空間幾何有是有幫助的,在下一篇文章「三度週期最小曲面的串珠模型(下)」中,我們將仔細解釋D與G兩種結構串珠模型的實作18。
n致謝
本文作者感謝臺灣大學新興物質與前瞻元件科技研究中心與量子科學與工程中心對於本計劃的支持,並感謝國科會支持我們持續在科學與藝術交叉領域中進行探索。
n參考文獻
1.Saranathan V.; Osuji, C.O.; Mochrie, S.G.; Noh, H.; Narayanan, S.; Sandy, A.; Dufresne, E.R. Proc. Natl. Acad. Sci. U S A. 2010, 107, 11676-81.
2.Schoen, A. H. NASA Technical Note No. D-5541, Washington DC, 1970.
3.Schoen, A. H. Interface Focus, 2012, 2 658-668.
4.Angew. Chem. Int. Ed. 2008, 47, 7996-8000.
5. 6.金必耀, 左家靜 珠璣科學系列 科學月刊 2012, 72-73, 230-233, 386-388, 556-558, 714-717.
7.金必耀, 莊宸, 左家靜 化學季刊 2008, 57, 316-324.
8.金必耀 化學季刊 2012, 70, 271-279.
9.Proceedings of Bridges: Mathematical Connections in Art, Music, and Science, 2012, 503-506.
10.2012 Joint Mathematical Meetings Exhibition of Mathematical Art, ed. by R. Fathauer and N. Selikoff, Tessellations Publishing 2012, 17.
11.Proceedings of Bridges: Mathematics, Music, Art, Architecture, Culture, 2010, 391-394.
12.Proceedings of Bridges: Mathematics, Music, Art, Architecture, Culture, 2011, 523-526.
13.The Beaded Molecules website, http://thebeadedemolecules.blogspot.com.
14.J. Chin. Chem. Soc. 2010, 57, 316-324.
15. 16.Proceedings of Bridges: Mathematical Connections in Art, Music, and Science 2013, 495-498.
17. 18.臺灣化學教育 2014。